-Tom
Welcome to the online content for Financial Mathematics for Cryptocurrencies. On this page, you will find more about the book and online resources for current and future readers.
About the book
Publication details
Title: Financial Mathematics for Cryptocurrencies
Editor: Wiley (Finance Series)
ISBN: 978-1-394-37007-8
Preface
Cryptocurrencies, and digital assets by extension, are stepping out of the shadowy corners of finance and going mainstream. What began as an ideological revolt against traditional banking institutions has become an instrument, like many others, to express one's view on the market and manage their risk.
When I began my career in the City[1], right after university, my first job offer was for a blockchain start-up. I decided then to go for a role in traditional finance (TradFi), and still have no regret. The decentralized finance (DeFi) industry, which represents digital assets in finance, had then a long way to go to mature and resolve systemic issues of corruption, money laundering, and other abhorrent malpractices. The air of rebellion and anti-establishment that was rife among the so-called "crypto bros" is slowly fading into a more measured, albeit daring, vision of what this new asset class can offer to investors and practitioners.
Digital assets are the promise that there is a new world beyond the digital frontier, one that allows for a comprehensive treatment of risk—without borders and excessive intermediation. This book is a message to fellow practitioners, in and outside DeFi, to continue to study, explore, and research this fascinating field.
As I write this book, I am not interested in settling the argument about the purpose of digital assets. Neither am I interested in promoting one ecosystem versus another. The fact is, cryptocurrencies are here and are mainstream. Another fact is, we, in TradFi, have observed them from afar and without the lenses of scientific curiosity which have propelled our industry in the past thirty years from an old boys' club to one of the most powerful instruments of economic development.
As quantitative analysts and traders, it is our duty to explore these assets without judgment and misconceptions. Only with knowledge can we ensure safe, efficient, and coherent financial systems. Censoring ourselves, withholding our expertise to certain parts of finance, leaves a vacuum that may be filled with misinformation and dangerous practices, which ultimately threaten the stability of the broader financial system. We might not like what we discover, or we might be excited about this brave new world. But we cannot afford to let one of the fastest-growing parts of how people exchange value fade into darkness. I was still a child during the Global Financial Crisis (GFC), but it has taught my generation that the well-functioning of the financial system is vital to our everyday lives. Healthy, prosperous economies demand reliable banks and payment networks, and digital assets can be instrumental where these are not yet in place.
I wrote the book I wish I had when I began exploring this digital world. We have many books about equities, fewer about derivatives, and less about foreign exchange. We let cryptocurrencies on the side and then did the same with NFTs. I am excited about bringing you on this journey of scientific curiosity. I hope I get challenged and maybe proven wrong in the theories I gathered in this book. But as long as we have an educated conversation, based on facts instead of beliefs, I am confident we can achieve greater shared prosperity—a financial system that can work for all.
This book would not have been possible without the incredible people I have met in my professional journey thus far. From London to Hong Kong, Dubai, and Singapore, I am proud of being part of a community of open-minded and curious practitioners who are all trying to answer collectively, "What can we do better?"
Tom J. Espel
Hong Kong, April 28, 2025
- The City of London is Europe's historical premier financial center. It comprises leading banking institutions, established in the historical boundaries of the "Square Mile" of the City of London and Canary Wharf. The term is a metonym for large, established financial institutions and the industry as a whole.
Table of Contents
Part I: Fundamentals of Digital Assets
Chapter 1. Overview of Digital Assets
- Semantics
- Brief History
- Major Coins
Chapter 2. Topology of Networks
- Blockchain Networks
- Sidechains
- Technical Characteristics
- Network Indicators
- Staking
Chapter 3. Asset Characteristics
- Network versus Asset
- Conventional Asset Classification
Part II: Network Valuation
Chapter 4. Digital Asset Classification
- Prudential Classification
- Sector Classification
- WWS Market Cap Characterization
- Ecosystem Classification
- Functional Classification
Chapter 5. Network Valuation
- Market Capitalization Multiple
- Business Valuations
- User-Based Network Valuations
- Discussion on Network Valuations
- Transaction Volume Pricing
- Factor Analysis
- Relative Value Pricing and Interchain Basis
Part III: Market Structure
Chapter 6. Carry and Storage
- Lending and Margin
- Carry and Forward Pricing
- Digital Asset Custody
Chapter 7. Liquidity Interface
- Traditional Finance Pathways
- Stablecoins
- Tokenized Assets
- DeFi Liquidity Interface
Chapter 8. Cost of Liquidity
- Price Decomposition Framework
- Components of the Spread
- The Blockchain Paradox
Chapter 9. Fee Models
- Fees
- Oscillating Fees Model
- Extended Fee Models
Part IV: Price Returns
Chapter 10. Price Process
- Mathematical Framework for Price Processes
- Price Returns
- Empirical Properties of Financial Time Series
Chapter 11. Price Return Models
- AR Models
- Constant Volatility Models
- Stochastic Volatility Models
Part V: Pricing Theory
Chapter 12. Discounting and Staking
- Clocks
- Pricing Assumptions
Chapter 13. Forward Rate Curve
- Rates and Curves
- Zero-Coupon Bond (ZCB)
- Interest Rate Curve
- Interest Rate Swap (IRS)
Chapter 14. Arbitrage Pricing Theory
- Numéraire
- Martingales
- Risk-Neutral Measure
- Money Market Account
- Validator Account
- Stablecoins
Chapter 15. Cross-Chain Asset Pricing
- On-Off-Chain Pricing
- Siegel Paradox
- Interchain Valuation
Chapter 16. Overview of Interest Rate Models
- CIR Model
- SABR Model
- SVJC Model
- HJM Model
Part VI: Staking Contract
Chapter 17. Direct Staking Contracts
- Direct Staking
- With Accrual
- Non-Accrual
- Non-Accrual with Queue Mechanisms
Chapter 18. Other Staking Contracts
- Liquid Staking
- Liquid Restaking
- Yield Farming
Afterword
Digital assets are such a fascinating field. I hope this book helps you explore it further.
In this work, we have made several key contributions to decentralized finance (DeFi) pricing theory. We have made the explicit distinction between the value of a blockchain and the value of its assets. We have highlighted three essential constructs for pricing in DeFi: the network time, the validator account, and the wrapped token. Network time reflects the blockchain-specific temporal framework that affects all pricing models. The validator account serves as a new numeraire for DeFi pricing theory under a B-measure for blockchain assets. Wrapped tokens enable cross-chain pricing and require new mathematical frameworks for proper valuation.
Together, these concepts allow us to bridge the current body of traditional finance (TradFi) knowledge, in particular arbitrage pricing theory, to DeFi.
However, in developing these tools, we must remember a fundamental truth about our discipline. Too often, quantitative analysts obsess and debate over what could be a perfect model. Such a pursuit is an illusion. Although the object of our field is scientific rigor, our subject remains the study of apparent chaos.
This book also faces the challenge of serving three audiences at once: practitioners want tools, traders want insights, and academics want rigor. As a practitioner, not an academic, I am acutely aware of the limitations of models, as much as I am convinced of the soundness of scholarly research.
Quantitative finance is a science that provides a framework, not absolute truths. We might find a perfect model, but in the presence of randomness, we would need an infinite amount of time to observe its outcome accurately. And, even if a "true" model were indeed to be found, with an accurate fair price, there is no guarantee that markets will eventually trade at such value. Consequently, pragmatic approaches will continue to prove more valuable than abstract theory. This is even more critical in the fast-changing world of DeFi.
In this spirit, I wrote this book for those who have the humility to learn and grow, those who understand that curiosity drives us to better understand how markets really work. In finance, the stakes are high and the impact of our industry on society is significant.
Too often, we are scared to challenge established norms and explore new ideas. When there is doubt and misunderstanding, the fear of being wrong prevents us from asking the right questions. I wish many books follow, that new theories will emerge, and that the scientific conversation will follow its course.
I hope future works will deepen areas this volume could only introduce. The breadth attempted here provides a map; and I encourage others to chart specific territories in greater detail.
Thank you for the time you invested in reading my book. Gathering theories and formulating new frameworks in this emerging field has been an exciting challenge.
We are at the dawn of a new era in quantitative finance; and your actions, not just your ideas, will shape the future of our industry. With DeFi growing, a new breed of quants, the B-quants, emerge alongside the P and Q-quants. I am excited about the contributions you will make, and I look forward to seeing what you will bring to this field.
Open problem hints
Each section of the book contains open problems. While there is no "firm" solution, I share below how I would go about approaching each of them.
Part I. Fundamentals
Problem I.1. We can first apply the reasoning on the sidechain.
- What are the implications for monetary emission?
- What are the implications for the locked collateral?
- Can the sidechain continue to operate independently?
The key is to understand that since the sidechain is actually a different blockchain, the problem is symmetrical.
Problem I.2. We first must discuss the interactions of Layer 1 and Layer 2 during congestions. Once that is done, we can analyze the specific implications for the pegged sidechain.
Problem I.3. We can begin by assuming the opposite, when the sidechain moves to PoS while the mainnet remains on PoW. We suggest considering the following elements.
- What are the consequences of differences in monetary emission mechanisms for the peg?
- How will the different finality guarantees and security models affect the bridge operation?
We can flip the reasoning to answer the original question, by highlighting how the bridges PoS to PoW and PoW to PoS will differ.
Problem I.4. It is clear that the difference between the two options arises from the tracking of the underlying cryptocurrency by the perpetual future.
- Which of the two underlyings is more volatile?
- Which of the two options do you expect to have a higher implied volatility?
We can also explore under the angle of market dynamics, with supply and demand.
- What are the first-order effects at maturity if there is a divergence between the spot price and the perpetual future price?
- What is the second-order effect of this divergence, if the option on the perpetual future represents material market volumes?
Part II. Network valuation
Problem II.1. Think in terms of number of users and their engagement with the platform. Using ZBOT, how does the network value change? Is it realistic to expect a sudden change in the value of the blockchain?
Problem II.2. If one person controls 1000 wallets, should N = 1 or N = 1000? Consider the usage of each wallet. What definition of N would make ZBOT Law resistant to manipulation?
Problem II.3. We must usually consider in such circumstances the liquidity of each wrapped token. If both have similar liquidity, then the discount could be linked to custodian risk.
Problem II.4. Begin first assuming from the perspective of the blockchain with the smallest value. User-valued valuations are adequate from this analysis. Is its value going up or down? What risks does it introduce? How about the other blockchain?
Part III. Market structure
Problem III.1. Note that the strategy is self-defeating, because it will increase transactions in the fee dips and decrease transactions in the fee peaks.
Problem III.2. Go back to the definition of convenience yield and reason in terms of pure economic benefit. When the convenience yield is positive, what does it mean? If it is negative, what variable needs to be adjusted? How can this situation arise? Think in terms of contango and backwardation.
Problem III.3. There are two ways to approach the problem.
- Who triggers the liquidations and for what purpose?
- Which position profits the most during market downturns?
Are all market participants honest with their intentions?
Problem III.4. Assume one blockchain has higher fees than the other.
- Which of the two is best for redemption?
- Which of the two is best for creation?
- How should the allocation change throughout the life of the ETF?
Problem III.5. This problem is about comparing physical cost of carry and cost of tokenization. What are the risks in either case? Consider factors such as liquidity, market depth, and the potential for slippage during redemptions and creations of the wrapped token.
Part IV. Price returns
Problem IV.1. This question is about if the choice of price return representation matters in extreme circumstances. What is the asymptotic behavior of these functions for large variations? Where do they differ the most?
Problem IV.2. We assume most stablecoins are pegged, and should therefore mean-revert, which is the Noah effect. What happens when the peg breaks?
Problem IV.3. How does leverage impact a crash? How does liquidation impact the price of the wrapped token? Think in terms of circuit breakers for trading in TradFi.
Problem IV.4. Which model assumes stationarity and which one does not? How does it impact the observation window, and trading window?
Part V. Pricing theory
Problem V.1. Try to price the continuously compounding VA under that modified numeraire.
Problem V.2. We must first notice that the mining rewards are not compounding, they are additive and do not scale. Can we use this numeraire? How can we express the relative price of an asset using this numeraire? Our objective is to explore why Theorem [ref] excludes miners from having a risk-free rate.
Problem V.3. Consider whether MEV revenues should be included in the validator account returns. Are these returns truly risk-free?
Problem V.4. We can first compare this probability measure versus 𝔹.
- Under the bullish measure, would expected returns still equal the staking rate?
- What happens to the no-arbitrage condition when investors have biased expectations?
- If all assets are expected to appreciate, what should be the appropriate numeraire to maintain martingale properties?
Problem V.5. We must first identify the numeraire on both blockchains. Then, we can compare the two and see how the carry opportunity would be affected by the different consensus mechanisms. Recall the Siegel paradox is about exchange rate volatility.
Problem V.6. Explore the relationship between transaction costs and the validator account.
Part VI. Staking contract
Problem VI.1. This paradox is all about understanding which time referential is used.
Problem VI.2. This problem is about understanding how a market would react to queues in staking.
- Assume no queues, is the natural state contango or backwardation?
- Assume queues are a fixed, predictable size. Would this impact the forwards?
Problem VI.3. Assume the opposite situation, where the LRT trades at a premium. What could explain this? What are the risks captured in the LRT? What does this mean for these AVS?
Problem VI.4. The paradox is that B has seemingly more uncertainty because of the queues, and yet there is a volatility compression. The idea is to compare how the underlying staking contract payout changes with and without the overrun. How are the boundaries of the payoffs changing?
Online content
In several parts of the book, I refer to online content that allows viewing some of the facts stated. I prefer to refer to live and interactive data, making full use of DeFi's data transparency, as opposed to printing out fixed charts.
Live chain explorers
Stablecoins on Ethereum
While ETH is the coin on Ethereum, several tokens can exist on a given blockchain. Ethereum has made such tokens popular with the introduction of ERC-20, and we can see that the most active tokens are linked to stablecoins.
Wallet explorers
This refers to Section 6.4.2.2. On both Bitcoin and Ethereum, the assets stored at a given address can be viewed publicly (note that one wallet may have multiple addresses). Unless the owner publicly states their address (e.g., exchanges) or links it to a domain name (such as Ethereum's ENS), the owner remains unknown.
Most of the largest wallets are held by exchanges, as one can see on the Bitcoin Rich List for Bitcoin. Etherscan also lists the top accounts on Ethereum.
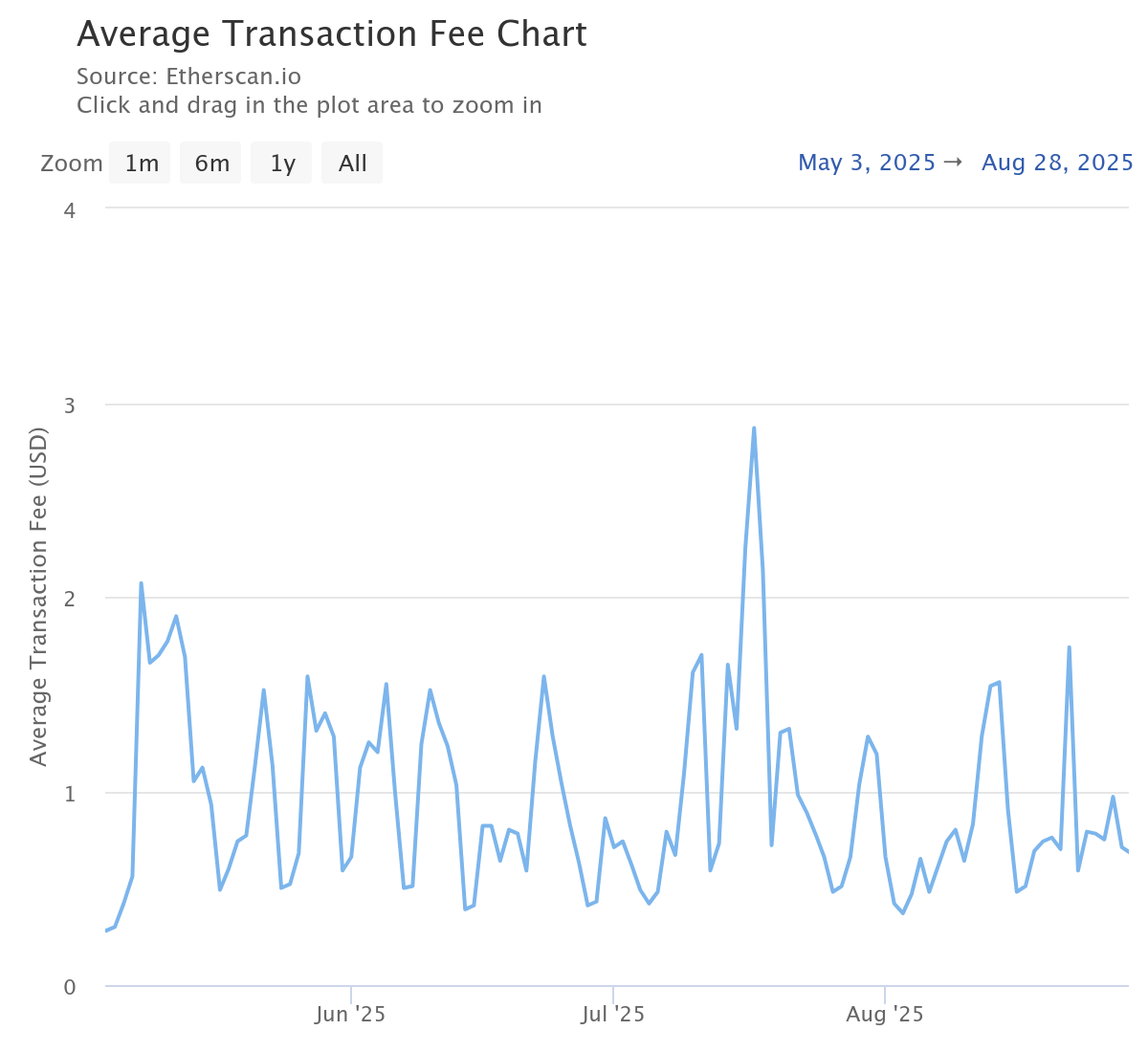
Ethereum network fees
This refers to Proposition 9.1 and Remark 9.4. Oscillations in the short term are clearly visible, in particular on median fees, on Bitcoin, and Ethereum. Note that the graphs are in USD, so some trends are linked to the exchange rate.
We can also see large spikes linked to network congestion (Blockchain Paradox), such as the one in May 2022 on Ethereum (see Etherscan).
Author's notes
The three most important takeaways from the book, which I refer to as the three contraptions, are as follows. Together, they allow us to reuse much of TradFi pricing theory in DeFi.
A time coordinate: the network time
One specific property of assets on blockchains is that transactions settle at the end of each block. For transactions on DEXes, prices are also agreed at the end of each block.
While for most blockchains the duration of blocks is stable, it is easier to switch to "network time", where each increment is one block time, for pricing. In network time, we can price with settlement times being certain.
A numéraire: the validator account
Arbitrage pricing theory for derivatives relies on the risk-neutral measure and the money market account (MMA) as a numéraire.
We construct an analogous concept, the validator account, and its corresponding blockchain measure B for pricing derivatives.
A bridge asset: the wrapped token
A convenient object in DeFi is the wrapped token, which represents an asset off-chain, or on another blockchain, on a given blockchain. This allows for constructing derivative contracts and decomposing risks.
We use the wrapped token construction for any asset that is non-native, including stablecoins.
I take the opportunity to discuss in a bit more detail some of the writing and editing choices I made in the writing of the book.
Network valuation
The book emphasizes important distinctions between network valuation and asset valuation. This is, admittedly, unusual for books in mathematical finance, which mostly ignore the former and leave it to corporate finance. However, in DeFi, the prominence of networks has often been characterized by the market capitalization of the networks, and the lines are blurred among practitioners. This is why I decided to dedicate one of the six parts of the book specifically to the valuation of networks as a whole. While several valuation techniques require approximation and judgement, one in particular - ZBOT's law - stands out as particularly adequate.
Fees and blockchain paradox
A distinctive feature of DeFi is that network fees are not akin to conventional spreads in TradFi. The latter are often waived away in the literature, as a result of market inefficiency and illiquidity. This is true in many cases, since more liquid markets become more competitive and fees decrease.
In DeFi, fees are actually set by the protocol. Changes in liquidity, efficiency, or infrastructure will only have a limited impact. This is why I decided to treat them explicitly and even provided a simple model for these fees.
Another interesting parameter is that in the very short term, increased activity leads to increased fees. While this is also true in TradFi, it is more pronounced in DeFi and is also agnostic to the direction of prices. This is what I refer to as the Blockchain Paradox, whereby the network will itself encourage stability of activity.
Interest rate models
I chose to keep Chapter 16 "Overview of Interest Rate Models" as an overview, with limited mathematical developments. Most notably, I did not explicitly define the HJM model; instead, I listed its properties. I made that call for four reasons.
- There is no difference between the formulation of these models in DeFi and in TradFi, and I refer to the reference material, which covers these topics;
- Practical implementations already exist in standardized libraries, and practitioners need only to know properties of the models and not re-code them;
- I believe that models more tailored to cryptocurrencies, such as the SVJC model, which I developed in that chapter, will emerge over time;
- Some of the theoretical background needed for a rigorous introduction was out of the scope of this introductory book.
However, I felt that it was appropriate to show explicit implementations of interest rate theory and give some pointers on how such models should be adapted to digital assets.
A notable decision I made when writing this book, in particular part V, was not to attend too much to the classical theoretical developments associated with changes of measure.
Measure theory
The classical introduction of the change of numéraire in mathematical finance is to develop measure theory with the introduction of probability spaces and the construction of the corresponding measure.
I made the choice not to discuss these topics for two reasons.
- Other books in TradFi offer such developments, which are not specific to DeFi, and I did not believe reusing the same type of developments would add value in an introductory book;
- While the approach is mathematically robust, I do not believe it is intuitive to modern students in mathematical finance. My preference was to emphasize the change of measure in the context of on-chain versus off-chain.
This is why I do not introduce Girsanov's theorem, nor the associated Radon-Nikodym derivative.
Validator account as a valid numéraire
I provide a rigorous, and mathematically comprehensive, introduction to the validator account in a separate paper.
I also wish, as an author, to help and inspire other authors and scientists to make a responsible yet productive use of new AI tools. I hope more authors share best practices, so we can collectively know how to make the most of these tools.
How to use AI responsibly
As of when I wrote the book, AI tools were overall quite poor when it comes to anything beyond basic editing of books, in particular, spelling and grammar. When it comes to Math, these tend to be consistently wrong, let alone when the concepts introduced are novel and outside their knowledge base. There is a pitfall that we believe was spun out of an AI is "true". But beyond being wrong, AI also introduces significant risks of plagiarism and logical incoherence.
AIs, and LLMs in particular, are good critics of style, but poor assessors of facts. By construction, they write "the most likely next sequence of words". If they are trained on erroneous or non-rigorous datasets, they are limited in assisting with scholarly, expert work.
My recommendation to students and other researchers is to view AIs are research assistants. They can prepare data and help with coding an idea, but need robust direction and constant fact-checking. In my case, as I tend to write a lot on paper and am not too confident in LaTeX's TikZ package for graphs, AI has been great.
Recommended AI tools
I wrote the manuscript in LaTeX using VS Code, with Copilot's auto-complete for code.
AI can be very helpful to pick up spelling and grammar mistakes (Grammarly and Claude in my case). I would, however, often have to instruct it not to make any edits to the equations.
Another powerful tool is NotebookLM, which I use to check for correct attribution. One can upload a set of papers or books as PDFs, and for a given statement, check that the correct document is assigned. The tool allows you to check for yourself in the source file.
My advice is simple: "Be transparent, and always check".
Further reading
First and foremost, on the "inspiration" side, I would like to point out some of the major works in quantitative finance. Although they are more applicable to TradFi, they have a significant influence on our field.
TradFi references
See my bookshelf with reference textbooks for students and practitioners.
Rough volatility
Rough volatility is one of the most trending topics in financial mathematics since the mid-2010s. It all began with the eponymous paper by Gatheral, Jaisson, and Rosenbaum in 2014; it has since grown into an active research community.
Most of the historical models of volatility, including those discussed in the book, are "smooth", using Brownian motions. This does not fit well with observations, where paths are more "rough", typically by introducing fractional Brownian motions.
For a more comprehensive overview, readers can review ICL's workshop slides. A notable application of the theory to computing is Dr Horvath's (lecture on YouTube).
There are other notable works, a bit beyond traditional mathematical finance, which I wish to share. These are the works from which I drew the quotes at the opening of each part of the book (except the first one!). I made a point to only select recent works, which I believe are part of the future standard body of knowledge for our line of work.
Beyond mathematical finance
Howard Marks, The Most Important Thing (2011). Marks, a famous investor and fund manager, offers a part-memoir, part-investment guide to the readers. I view it as a modern and short version of Graham and Dodd's classic Securities Analysis (1934), as if it were written in our times. It is a high-level and gentle introduction to investing and finance. How Marks develops his rationale and philosophy about risk is notable for its clarity and simplicity.
Ray Dalio, Principles: Life and Work (2017). Neither the author nor the book needs an introduction. It's bite-sized, it's straight to the point, and it's an enjoyable read.
Annie Duke, Thinking in Bets (2019). Duke's a former top-level poker player, and her best-selling book is a simple and yet thorough explanation of probabilistic thinking. Probabilistic thinking is at the heart of trading, in particular, high-frequency trading. I recall that this book had a significant influence on me when I started my own career, despite its main topic not being finance. In recent years, more and more finance professionals have turned to Duke's work. My bet is that this book will age well and will become a modern classic in finance, alongside Michael Lewis' works.
Nassim N. Taleb, The Bed of Procrustes (2010). The third and shortest opus of Taleb's quintet is often overlooked. It is less famous than its masterpiece, The Black Swan (2007), and is the least mathematical of the five. However, I find this collection of quotes, reminiscent of Blaise Pascal's famous Pensées (1670), very insightful into Taleb's mindset. It's a short read, and, as one can expect from the author, quite witty.
Nate Silver, On the Edge (2024). The book can be summarized by its subtitle: "The art of risking everything. Silver is the founder of FiveThirtyEight, a pioneering political analysis website that has had a significant influence on both DeFi, including modern prediction markets, and its associated philosophical movements, such as Rationality. Notable contributions of Silver are his definition of the "river" as those who master risk and live on the edge of uncertainty. My autographed edition of the book is one of my most treasured pieces, and it resonates well with Duke's and Rubin's works.
